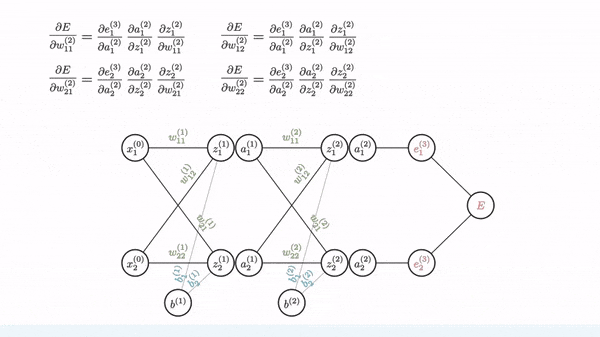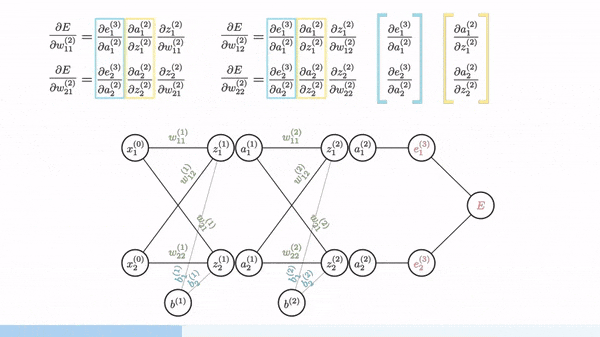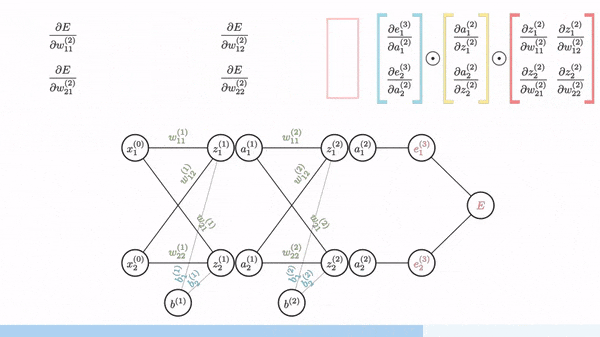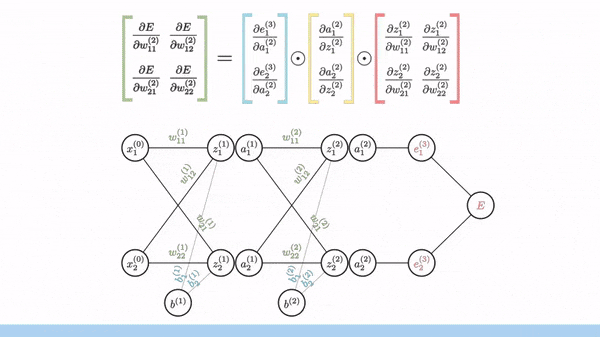
import numpy as np
class NumpyNeuralNetwork:
# Here we define the number and types of layers in our network
# we also include their activation functions
# TODO: You'll almost certainly need to add some more layers to get to 70% accuracy
NN_ARCHITECTURE = [
{"input_dim": 784, "output_dim": 37, "activation": "relu"},
{"input_dim": 37, "output_dim": 26, "activation": "softmax"},
]
# Our init function just initializes the weights and biases for each layer
def __init__(self, seed = 42):
# random seed initiation
np.random.seed(seed)
# parameters storage initiation
self.params_values = {}
# iteration over network layers
for idx, layer in enumerate(self.NN_ARCHITECTURE):
# we number network layers from 1
layer_idx = idx + 1
# extracting the number of units in layers
layer_input_size = layer["input_dim"]
layer_output_size = layer["output_dim"]
# initiating the values of the W matrix
# and vector b for subsequent layers
self.params_values['W' + str(layer_idx)] = np.random.randn(
layer_output_size, layer_input_size) * 0.1
self.params_values['b' + str(layer_idx)] = np.random.randn(
layer_output_size, 1) * 0.1
def get_params_values(self):
return self.params_values
# TODO: Write the relu function
def relu(self, Z):
"""
Applies the ReLU (Rectified Linear Unit) activation function.
Inputs:
- Z: NumPy array of pre-activation values from a layer
Returns:
- A: NumPy array with ReLU outputs
Concept Check: Why is Z in a perceptron a number but Z in a neural network is a matrix of numbers?
Concept Check: What are the dimensions of the Z vector? Don't answer with a specific number but a generalizable statement
"""
return None
# TODO: Write the relu_backward function
def relu_backward(self, dA, Z):
"""
Perform the backward pass for the ReLU activation function.
Inputs:
- dA: Gradient of the loss with respect to the activation output (A) from the current layer
- Z: The input to the activation function of currently layer
Returns:
- dZ: Gradient of the loss with respect to the input (Z) of the current layers ReLU activation function
Concept Check: What is the purpose of setting the gradient dZ to 0 for elements where Z≤0 in the ReLU backward function?
Concept Check: What is the calculated dZ (the returned matrix) of this function used for?
"""
return None
# TODO: Write the softmax function
def softmax(self, Z):
"""
Computes the softmax activation function for the given input Z.
Inputs:
- Z : Input matrix to the softmax function
Returns:
- A probability distribution representing the likelihood of each class
Concept Check: What does the softmax function do and where is it normally used in a neural network?
"""
return None
# TODO: Write the softmax_backward function
def softmax_backward(self, dA, Z):
"""
Computes the gradient of the loss with respect to Z for a softmax activation function.
Inputs:
- dA: Gradient of the loss with respect to the output of the softmax layer
- Z: Input to the softmax function before activation
Returns:
- Gradient of the loss with respect to Z
"""
# Hint: for cross entropy loss function, softmax_backwards becames very simple (1 line)
return None
# TODO: Finish the single_layer_forward_propagation function
def single_layer_forward_propagation(self, A_prev, W_curr, b_curr, activation="relu"):
"""
Performs forward propagation for a single layer.
Parameters:
- A_prev: Activation from the previous layer
- W_curr: Weights for the current layer
- b_curr: Biases for the current layer
- activation: Activation function to apply
Returns:
- A: Activation output of the current layer
- Z_curr: linear transformation result before activation
Concept Check: Why do we return both A and Z_curr?
"""
# TODO: calculation of the input value for the activation function
# hint: this looks super similar to the perceptron equation!
Z_curr = None
# selection of activation function
if activation == "relu":
activation_func = self.relu
elif activation == "sigmoid":
activation_func = self.sigmoid
else:
raise Exception('Non-supported activation function')
# TODO: return of calculated activation A and the intermediate Z matrix
return None
# TODO: Finish the full_forward_propagation function
def full_forward_propagation(self, X):
"""
Performs forward propagation through the entire neural network.
Inputs:
- X : input data
Returns:
- A_curr : final activation output of the network
- memory : dictionary storing intermediate A and Z values for backpropagation
"""
# creating a temporary memory to store the information needed for a backward step
memory = {}
# X vector is the activation for layer 0
A_curr = X
# iteration over network layers
for idx, layer in enumerate(self.NN_ARCHITECTURE):
# we number network layers from 1
layer_idx = idx + 1
# transfer the activation from the previous iteration
A_prev = A_curr
# TODO: extraction of the activation function for the current layer
activ_function_curr = None
# TODO: extraction of W for the current layer
W_curr = None
# TODO: extraction of b for the current layer
b_curr = None
# TODO: calculation of activation for the current layer
A_curr, Z_curr = None
# saving calculated values in the memory
memory["A" + str(idx)] = A_prev
memory["Z" + str(layer_idx)] = Z_curr
# return of prediction vector and a dictionary containing intermediate values
return A_curr, memory
def get_cost_value(self, Y_hat, Y):
"""
Computes the cost of the neural network's predictions
Inputs:
- Y_hat: The predicted probabilities
- Y: ground truth labels
Output:
- The computed loss
Concept Check: What are the dimensions of Y_hat and Y?
"""
# number of examples
m = Y_hat.shape[1]
# calculation of the cost according to the formula
cost = -1 / m * (np.dot(Y, np.log(Y_hat).T) + np.dot(1 - Y, np.log(1 - Y_hat).T))
return np.squeeze(cost)
# TODO: Write the convert_prob_into_class function
def convert_prob_into_class(self, probs):
"""
Converts probability values from the softmax function into discrete class predictions
Inputs:
- probs : 2D array where each col represents the predicted probability distribution
over classes for a given example
Output:
- probs_ : 1D array where each value represents the predicted class for each example
"""
probs_ = np.copy(probs)
pass
return probs_.flatten()
def get_accuracy_value(self, Y_hat, Y):
"""
Computes the accuracy of the model's predictions by comparing them with the true labels
Inputs:
- Y_hat:
- Y:
Output:
- The accuracy of the model’s predictions, which is the fraction of correctly predicted labels
"""
Y_hat_ = self.convert_prob_into_class(Y_hat)
return (Y_hat_ == Y).all(axis=0).mean()
# TODO: Write the single_layer_backward_propagation function
def single_layer_backward_propagation(self, dA_curr, W_curr, b_curr, Z_curr, A_prev, activation="relu"):
"""
Performs backward propagation for a single layer to calculate the gradients of the cost function
with respect to the weights, biases, and activations
Inputs:
- dA_curr: The gradient of the loss with respect to the activation output (A) from the current layer
- W_curr : The weights for the current layer
- b_curr : The biases for the current layer
- Z_curr : The linear transformation result (Z) before activation for the current layer
- A_prev : The activation from the previous layer
- activation : The activation function used in the current layer ("relu" or "sigmoid")
Output:
- dA_prev : The gradient of the loss with respect to the activation of the previous layer (used for backpropagation)
- dW_curr : The gradient of the cost function with respect to the weights (used for weight updates)
- db_curr : The gradient of the cost function with respect to the biases (used for bias updates)
Concept Check: What is the significance of calculating dW_curr in backpropagation?
Concept Check: After calculating the gradients for weights (dW_curr) and biases (db_curr), what is the purpose
of the calculation dA_prev used for in backpropagation?
"""
# number of examples
m = A_prev.shape[1]
# selection of activation function
if activation == "relu":
backward_activation_func = self.relu_backward
elif activation == "sigmoid":
backward_activation_func = self.sigmoid_backward
else:
raise Exception('Non-supported activation function')
# TODO: calculation of the activation function derivative
dZ_curr = None
# TODO: derivative of the matrix W
dW_curr = None
# TODO: derivative of the vector b
db_curr = None
# TODO: derivative of the matrix A_prev
dA_prev = None
return dA_prev, dW_curr, db_curr
# TODO: Finish the full_backward_propagation function
def full_backward_propagation(self, Y_hat, Y, memory):
"""
Performs the backward propagation through the entire neural network.
Inputs:
- Y_hat: the predicted values (activations)
- Y: ground truth labels (one-hot encoded)
- memory: dictionary containing the activations and pre-activations (Z values)
for each layer during the forward pass.
Outputs:
- grads_values: dictionary containing the gradients of the cost function
with respect to the weights, biases, and activations for each layer.
Concept Check: Why store the calculated gradients in a dictionary? How will they be used?
"""
grads_values = {}
# number of examples
m = Y.shape[1]
# a hack ensuring the same shape of the prediction vector and labels vector
Y = Y.reshape(Y_hat.shape)
# TODO: initiation of gradient descent algorithm
# hint: The initial gradient of the loss with respect to the activation can be set up using only the the predicted labels, true lables, and one mathmatical operator
dA_prev = None
# iteration over network layers
for layer_idx_prev, layer in reversed(list(enumerate(self.NN_ARCHITECTURE))):
# we number network layers from 1
layer_idx_curr = layer_idx_prev + 1
# extraction of the activation function for the current layer
activ_function_curr = layer["activation"]
dA_curr = dA_prev
# We get the activation from the previous layer and the Z matrix from the current layer
A_prev = memory["A" + str(layer_idx_prev)]
Z_curr = memory["Z" + str(layer_idx_curr)]
# We get the weights and biases for the current layer
W_curr = self.params_values["W" + str(layer_idx_curr)]
b_curr = self.params_values["b" + str(layer_idx_curr)]
# TODO: calculate the gradients of the cost function with respect to the weights and biases
dA_prev, dW_curr, db_curr = None
# We save the gradients of the cost function with respect to the weights and biases
grads_values["dW" + str(layer_idx_curr)] = dW_curr
grads_values["db" + str(layer_idx_curr)] = db_curr
return grads_values
def update(self, grads_values):
"""
Updates the weights and biases of the neural network during gradient descent.
Inputs:
- grads_values: dictionary containing the previously calculated gradients
Outputs:
- params_values: dictionary containing the updated values of the weights and biases
"""
# iteration over network layers
for layer_idx, layer in enumerate(self.NN_ARCHITECTURE, 1):
self.params_values["W" + str(layer_idx)] -= self.learning_rate * grads_values["dW" + str(layer_idx)]
self.params_values["b" + str(layer_idx)] -= self.learning_rate * grads_values["db" + str(layer_idx)]
return self.params_values
# TODO: Finish the train function
def train(self, X, Y, epochs=100, learning_rate=0.01, batch_size=8, verbose=False):
"""
Train the neural network using mini-batch gradient descent
Inputs:
- X: Input data (features), shape (n_features, n_examples)
- Y: True labels, shape (n_classes, n_examples)
- epochs: Number of training iterations
- learning_rate: Learning rate for gradient descent
- batch_size: Size of each mini-batch
- verbose: If True, prints cost and accuracy at intervals
Outputs:
- Dictionary containing cost and accuracy history over epochs
"""
# initiation of lists storing the history of metrics calculated during the learning process
cost_history = []
accuracy_history = []
m = X.shape[1]
# TODO: implement mini-batch training
for i in range(epochs):
# Mini-batch processing
permutation = np.random.permutation(m)
X_shuffled = X[:, permutation]
Y_shuffled = Y[:, permutation]
for j in range(0, m, batch_size):
#TODO: Forward propagation
pass
#TODO: Backward propagation
pass
#TODO: Update parameters
self.update(grads, learning_rate)
# TODO: Calculate metrics for the whole epoch (cost and accuracy)
# Append metrics to storage
cost_history.append(cost)
accuracy_history.append(accuracy)
if verbose and i % 500 == 0:
print(f"Epoch {i+1}/{epochs}")
print(f"Cost: {cost:.5f}")
print(f"Accuracy: {accuracy:.5f}")
print("-" * 30)
return {'cost_history': cost_history, 'accuracy_history': accuracy_history}
# Comment to prevent docstrings from being printed